SOLUTION 5
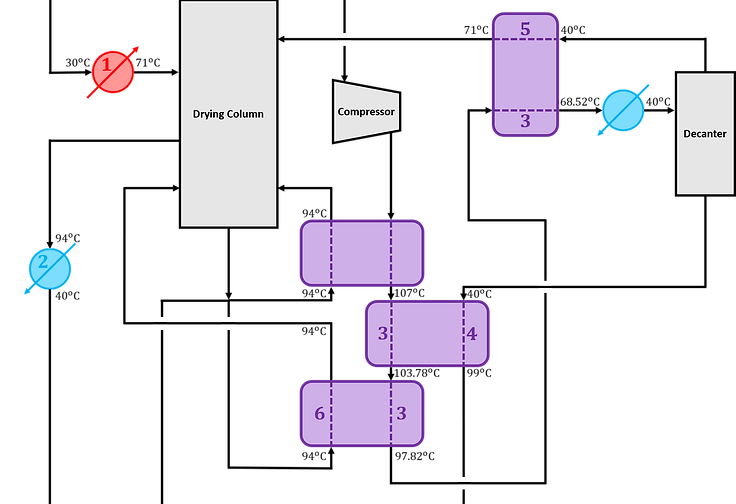).png)
3''
5
3 4
6 3'
Preexisting
heat exchanger
Heat exchanger (3-4)
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
Stream 3
Heat capacity*Mass flowrate
40.3 kW/°C
Heat gained by system
-2700.1 kJ/s
Temperature in
107°C
Temperature out
40°C
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
Stream 4
Heat capacity*Mass flowrate
2.2 kW/°C
Heat gained by system
129.8 kJ/s
Temperature in
40°C
Temperature out
99°C
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
Heat exchanger
Remaining heat
2570.3 kJ/s
Temperature Hot out
103.78°C
Log mean Temperature
26.89°C
We now seek to find the maximum amount of heat that can be exchanged between stream 3 and stream 4. This maximal amount corresponds to the lowest value of the absolute value of heat gained by the system between stream 3 and 4.
From that we calculate the remaining heat that needs to be removed
And the effective temperature out of Stream 3
Finally, we calculate the log mean temperature using the formula
Cost
Cross sectional area
5.62m²
Costs
5 633£
Variance on cost
±845£
We first calculate the area required for the heat exchanger based on this equation:
where U represents the overall heat transfer coefficient
and Q represents the actual amount of heat tranferred between the two streams above.
We then calculate the cost using the following formula:
%
Heat exchanger (3'-6)
Stream 3'
Heat capacity*Mass flowrate
40.3 kW/°C
Heat gained by system
-2570.3 kJ/s
Temperature in
103.78°C
Temperature out
40°C
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
Stream 6
Latent heat of vaporisation
2000 kJ/kg
In stream 6, the substance goes through a phase change whilst remaining at 94°C. We thus use the formula:
We know that the massflowrate is 12kg/s. Additionally, we know that the specific latent heat of vaporisation is 2000kJ/kg.
We thus plug in the numbers and find that
Heat gained by system
240 kJ/s
Mass flowrate
0.12 kg/s
Phase Change
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
Heat exchanger
Remaining heat
2330.3 kJ/s
Temperature Hot out
97.82°C
Log mean Temperature
6.34°C
We now seek to find the maximum amount of heat that can be exchanged between stream 3' and stream 4. This maximal amount corresponds to the lowest value of the absolute value of heat gained by the system between stream 3' and 4.
From that we calculate the remaining heat that needs to be removed
And the effective temperature out of Stream 3' which we find to be equal to 97.82 degrees celcius.
Finally, we calculate the log mean temperature using the formula
Cost
Cross sectional area
44m²
Costs
19 370£
Variance on cost
±2 905£
We first calculate the area required for the heat exchanger based on this equation:
where U represents the overall heat transfer coefficient
and Q represents the actual amount of heat tranferred between the two streams above.
We then calculate the cost using the following formula:
%
Heat exchanger (3''-5)
Stream 3''
Heat capacity*Mass flowrate
40.3 kW/°C
Heat gained by system
-2330.3 kJ/s
Temperature in
97.82°C
Temperature out
40°C
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
Stream 5
Heat capacity*Mass flowrate
38.1 kW/°C
Heat gained by system
1181.1 kJ/s
Temperature in
40°C
Temperature out
71°C
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
We first calculate the heat gained by the system with the heaters in the plant using the formula:
We then calculate the temperature difference to plug into the equation
We find that
Heat exchanger
Remaining heat
1149.2 kJ/s
Temperature Hot out
68.52°C
Log mean Temperature
27.66°C
We now seek to find the maximum amount of heat that can be exchanged between stream 3'' and stream 5. This maximal amount corresponds to the lowest value of the absolute value of heat gained by the system between stream 3'' and 5.
From that we calculate the remaining heat that needs to be removed
And the effective temperature out of Stream 3'' is found to be 97.82 degrees celcius, using the same formula as previously stated
Finally, we calculate the log mean temperature using the formula and find
Cost
Cross sectional area
49.6m²
Costs
20 825£
Variance on cost
±3 124£
We first calculate the area required for the heat exchanger based on this equation:
where U represents the overall heat transfer coefficient
and Q represents the actual amount of heat tranferred between the two streams above.
We then calculate the cost using the following formula:
%
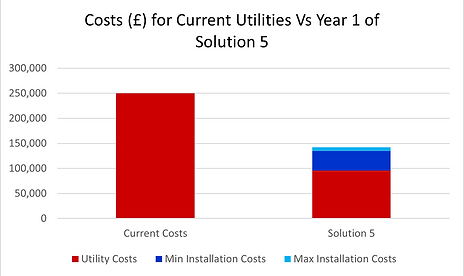
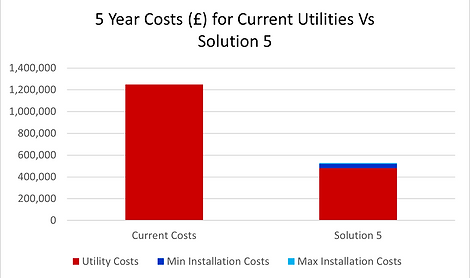
Overall cost
Money saved
723 400 ±6 800£
New total cost
527 000 ±6 800£
Utility cost (per year)
96 000£
Installation cost
45 800 ±6 800£
%
The total cost for this solution is the sum of the costs for utility over 5 years and the installation of the 3 heat exchangers.
Utility costs arise from the requirement for further heating or cooling once a stream has passed through a heat exchanger. If no exchanger is installed on a stream, utility costs for that flow will remain unchanged.
Cooling in this case (requires 2 coolers):
-
The temperature of Stream 2 needs to be reduced by 54.00 °C
-
The temperature of Stream 3 needs to be reduced by 28.52 °C
Heating in this case (requires 1 heater):
-
The temperature of Stream 1 needs to be raised by 41 °C
This gives rise to a total utility cost over 5 years of £481,000.
).png)
).png)